Optical initialization and readout of NV spins

from matplotlib import pyplot
import numpy as np

Introduction

The magnetic moment of an electron is called 'spin'. Just like a bar magnet, a spin wants to align with a magnetic field to lower its energy. The energy difference between the spin being aligned or anti-aligned with the field is called the Zeeman energy. How the Zeeman energy varies with magnetic field is known to a very large precision. Therefore, a measurement of this energy difference allows us to determine the magnetic field, which is the central concept of this lab course.

How can one measure the Zeeman energy of an electron spin? Firstly, it is important to realize that, at room temperature, the Zeeman energy is very small compared to the thermal energy $k_BT$. This implies that a spin in a material at room temperature continuously gets 'scrambled' through the contact with its hot environment, making it hard to determine its Zeeman energy.

Fortunately, the electron spin of the NV center has the property that it can be 'initialized' (polarized) using simple green laser excitation. In addition, laser excitation will make the NV center fluoresce (emit red photons) with a brightness that depends on its spin state. This optically-induced spin polarization and photoluminescence readout allows us to use the NV spin as a magnetometer.

Initialization and readout of the NV spin

We will now describe the mechanism by which the NV spin state polarizes into $m_S=0$ under optical excitation, and how the NV fluorescence depends on the spin state. On the following page, we will describe in detail how the energies of the NV spin states depend on the applied magnetic field.

The NV center has an $S=1$ electron spin. Therefore, it has 3 possible spin states, which we will label $m_S=0,−1,+1$. The optical initialization and read out of the NV spin can be understood from the following simplified energy level structure of the NV center:

fig = pyplot.figure()
ax = fig.add_subplot(111)
ax.plot([0.0, 0.5], [0.0, 0.0], 'k', linewidth=4)
ax.plot([0.0, 0.5], [0.12, 0.12], 'k', linewidth=4)
ax.plot([0.0, 0.5], [1.0, 1.0], 'k', linewidth=4)
ax.plot([0.0, 0.5], [1.12, 1.12], 'k', linewidth=4)
ax.plot([0.6, 1.1], [0.8, 0.8], 'k', linewidth=4)

ax.axis("off")

ax.set_xlim(0.0, 2.0);
ax.set_ylim(0.0, 1.3);
ax.set_axis_off();
ax.text(-0.15, -0.02, r'$m_s=0$', ha='center');
ax.text(-0.15, 0.10, r'$m_s=\pm 1$', ha='center');
ax.text(-0.36, 0.04, r'Ground state', ha='right');

ax.text(-0.15, 0.98, r'$m_s=0$', ha='center');
ax.text(-0.15, 1.10, r'$m_s=\pm1$', ha='center');
ax.text(-0.36, 1.04, r'Excited state', ha='right');

ax.axes.get_xaxis().set_visible(False);
ax.axes.get_yaxis().set_visible(False);
ax.text(0.75, 1.0, r'Spin-dependent decay to metastable state', ha='left');
ax.text(0.75, 0.4, r'Non-radiative decay to $m_s=0$', ha='left');

ax.text(0.13, 0.6, r' Spin-preserving', ha='right', color='g');
ax.text(0.13, 0.5, r'green laser excitation', ha='right', color='g');

ax.text(0.28, 0.6, r'Spin-preserving', ha='left', color='r');
ax.text(0.28, 0.5, r'radiative decay', ha='left', color='r');
ax.annotate("", xy=(0.85, 0.83), xytext=(0.53, 1.12), arrowprops=dict(arrowstyle="->"));
ax.annotate("", xy=(0.53, 0.0), xytext=(0.85, 0.77), arrowprops=dict(arrowstyle="->"));
ax.annotate("", xy=(0.18,1.11), xytext=(0.18, 0.13), arrowprops=dict(arrowstyle="->", color='g'));
ax.annotate("", xy=(0.14,0.99), xytext=(0.14, 0.01), arrowprops=dict(arrowstyle="->", color='g'));
ax.annotate("", xy=(0.26,1.11), xytext=(0.26, 0.13), arrowprops=dict(arrowstyle="<-", color='r'));
ax.annotate("", xy=(0.22,0.99), xytext=(0.22, 0.01), arrowprops=dict(arrowstyle="<-", color='r'));

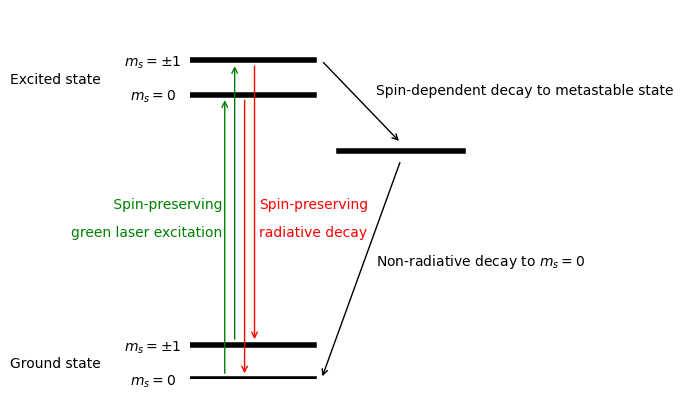
Fig. 2.1 - Electronic level structure of the NV center in diamond. The ground state of the NV center has three spin states with a zero-field splitting between the $m_s=0$ and the $m_s=\pm1$ states. Green-laser excitation leads to a red photoluminescence. The intensity of this photoluminescence is lower for the $m_s=\pm 1$ states due to a spin-selective, non-radiative decay channel. The spin-dependent photoluminescence enables us to detect the NV spin state optically. Moreover, the optical excitation polarizes the NV spin state because of the preferential decay from the metastable state into $m_s=0$

The level structure shows the electronic (orbital) ground and excited state of the NV center. Both of these have a splitting between their $m_S=0$ and $m_S=\pm1$ spin states that is present even at zero magnetic field (the 'zero-field splitting') (Fig. 2.1). Optical excitation (green arrows) preserves the spin state. The subsequent decay back to the ground state mostly occurs radiatively, emitting a red photon. However, decay can also occur non-radiatively via a metastable state. This non-radiative decay path is more likely to occur for the $m_s=\pm1$ states. As a result, the strength of the NV photoluminescence will depend on the original spin state, with $m_S = 0$ being the "bright" state and $m_S = \pm 1$ being the "dark" states. Finally, the decay from the metastable into the orbital ground state does not preserve the spin, but instead drives it into the $m_S=0$ state. This enables us to polarize the NV spin into the $m_S=0$ state (referred to as "optical spin polarization").

Exercise 2 - Optical spin readout

1. Explain in your own words the principle of the NV center's spin-dependent photoluminescence. In particular, discuss how the decay via the metastable state causes optical spin contrast (i.e., a difference in the photoluminescence for the $m_S=0$ and the $m_S=\pm1$ states.)
2. Discuss the excitation and decay process under continuous green laser excitation, and how this process eventually polarizes the NV spin into the $m_S=0$ state.